Brilliant Info About What Does Q Mean In Coulomb's Law

Unlocking Coulomb's Law
1. Charges, Forces, and a Little Bit of Physics Fun
Ever stared at a physics equation and felt like you were reading ancient hieroglyphics? You're not alone! Coulomb's Law, at first glance, might seem intimidating, but trust me, it's actually pretty cool once you understand the players. The 'q' in Coulomb's Law is a key player — it's what this whole article is about.
So, what does 'q' mean? In a nutshell, 'q' represents electric charge. It's a fundamental property of matter that causes it to experience a force when placed in an electromagnetic field. Think of it like this: some things just "feel" the electromagnetic field, and 'q' is the measure of how strongly they feel it. The 'q' is a noun, describing an amount of charge. We use Coulombs (C) to measure charge, named after the brilliant French physicist Charles-Augustin de Coulomb, the very guy who came up with the law in the first place.
You might encounter 'q1' and 'q2' in the formula. Don't panic! This simply indicates that there are two charges involved in the interaction you're studying. Imagine two balloons you've rubbed on your hair. Each balloon now has a charge, and 'q1' would be the charge on the first balloon, while 'q2' would be the charge on the second. It's like labeling your socks — helps keep things organized.
Now, charges can be positive or negative. Positive charges are typically associated with protons (found in the nucleus of an atom), and negative charges are associated with electrons (orbiting the nucleus). Opposite charges attract each other (positive pulls negative), and like charges repel each other (positive pushes positive, negative pushes negative). That's the fundamental principle at play in Coulomb's law, and 'q' helps quantify just how strong that attraction or repulsion is.

Delving Deeper
2. Why 'q' Matters in the Grand Scheme of Things
Understanding 'q' is more than just memorizing a formula. It's understanding the very fabric of how things interact at an atomic level. The amount of charge, or the magnitude of 'q', directly influences the strength of the electric force between charged objects. A larger 'q' means a stronger force, and vice versa. Think of 'q' as the "power level" of the charge; the bigger the power level, the more intensely it interacts.
Without electric charge, matter as we know it wouldn't exist. Atoms are held together by the electromagnetic force, which arises from the interactions between positive and negative charges. Molecules form because of the attractive forces between atoms, and these forces, again, are rooted in electric charge. Everything you see, touch, and interact with ultimately owes its existence to the fundamental property represented by 'q'.
Consider everyday phenomena. Static electricity, the kind that makes your hair stand on end when you take off a wool sweater, is a direct result of charge imbalance. The sweater rubs electrons off your hair, giving your hair a net positive charge. Since like charges repel, your hair strands push away from each other, leading to that delightful (or annoying) static cling.
Electrical devices, from your phone to your car, all rely on the controlled movement of electric charge. Batteries store chemical energy that can be converted into electrical energy, driving a current of electrons (negative charges) through circuits to power various components. So, the next time you use your phone, remember that 'q' is silently working behind the scenes, making it all possible.
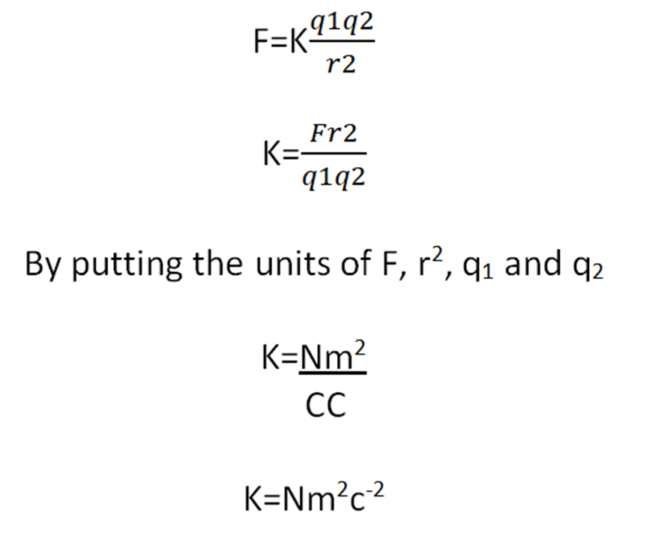
What Is Coulomb's Law? A Detailed Introduction
Coulomb's Law Formula
3. Putting It All Together
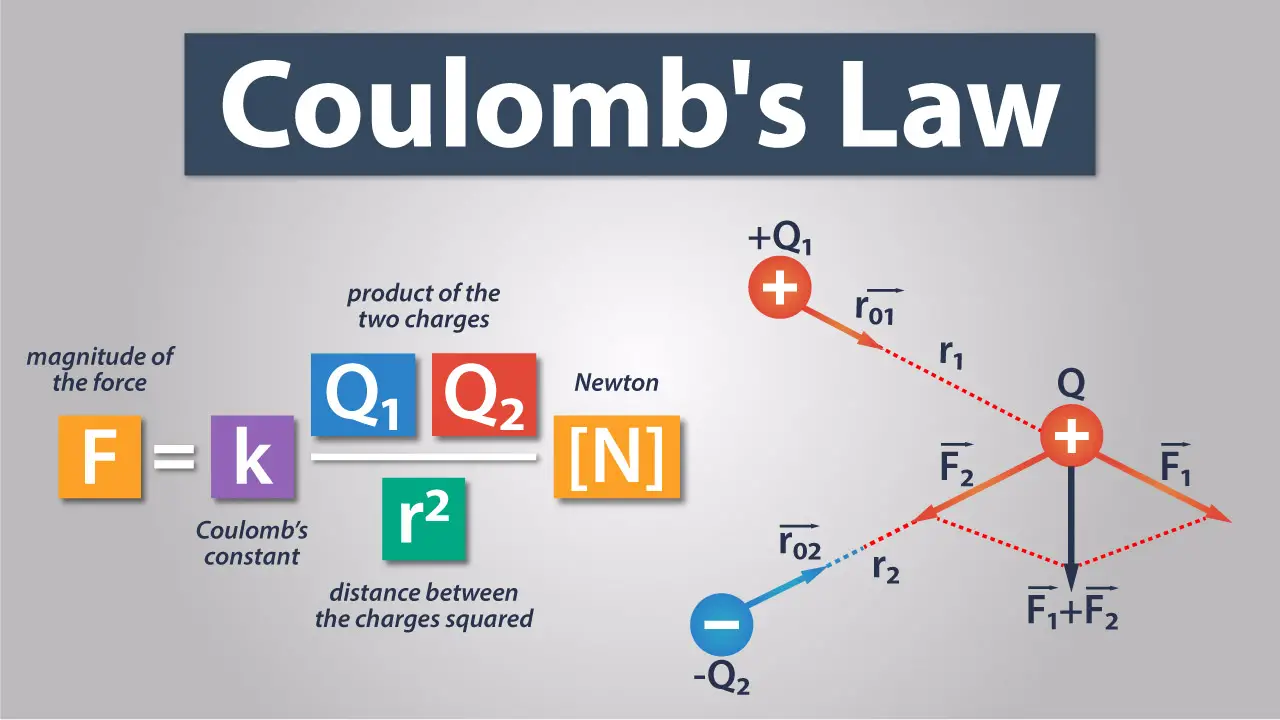
Okay, let's put 'q' into context within the actual Coulomb's Law formula. The equation is typically written as: F = k |q1 q2| / r, where:
- F is the electric force between the charges.
- k is Coulomb's constant (approximately 8.9875 10^9 Nm/C).
- q1 and q2 are the magnitudes of the charges.
- r is the distance between the centers of the charges.
The absolute value signs around 'q1 q2' indicate that we're only concerned with the magnitude of the force. The sign of the force (positive or negative) tells us whether it's attractive or repulsive. If 'q1' and 'q2' have the same sign (both positive or both negative), the force is repulsive. If they have opposite signs, the force is attractive. Simple enough, right?
Notice how the force is directly proportional to the product of the charges ('q1 q2'). This means that if you double the magnitude of one of the charges, you double the force. If you triple both charges, you increase the force by a factor of nine! It's a powerful relationship.
Also, take a look at 'r', the square of the distance between the charges. The force is inversely proportional to the square of the distance. This means that if you double the distance between the charges, you reduce the force by a factor of four. This is known as an inverse square law, and it's a fundamental concept in physics. Gravity works the same way!
Coulombs Law Credit Wikimedia User The Elementary Concept
Real-World Examples
4. From Balloons to Lightning
We've already touched on static electricity, but let's explore some other real-world examples where 'q' plays a crucial role. Consider electrostatics in photocopying and laser printing. Toner particles, which carry a specific charge ('q'), are attracted to oppositely charged areas on a drum. This allows the image to be transferred to paper and then fused in place with heat.
Lightning is another dramatic example of electric charge in action. During thunderstorms, charge separation occurs within clouds, creating large regions of positive and negative charge. When the electric field becomes strong enough, it overcomes the insulating properties of the air, and a massive discharge of electricity (lightning) occurs, neutralizing the charge imbalance. The amount of charge transferred in a lightning strike can be enormous!
Another, less dramatic, example involves capacitors. Capacitors are electronic components that store electrical energy by accumulating electric charge on two conductive plates separated by an insulator. The amount of charge a capacitor can store is directly proportional to the voltage applied across its plates. Capacitors are used in a wide variety of applications, from smoothing out voltage fluctuations in power supplies to storing energy in defibrillators.
Even in the realm of chemistry, 'q' is essential. The formation of chemical bonds between atoms involves the sharing or transfer of electrons (negative charges). Ionic bonds, for example, are formed when one atom transfers electrons to another, creating ions with opposite charges that attract each other. The strength of these bonds depends on the magnitude of the charges involved.

Coulomb's Law, Electrostatic Force, Electricity & Physics
Frequently Asked Questions (FAQs) About 'q' in Coulomb's Law
5. Quick Answers to Common Questions
Still have questions about 'q'? Here are some frequently asked questions to help clarify things:
Q: What are the units for 'q'?A: The unit for electric charge ('q') is the Coulomb (C).
Q: Can 'q' be zero?A: Yes, an object can have a net charge of zero if it has an equal number of positive and negative charges. This doesn't mean it has no charges at all, just that they are balanced.
Q: Is 'q' a vector or a scalar quantity?A: 'q' is a scalar quantity, meaning it only has a magnitude (amount) and no direction. The electric force, on the other hand, is a vector quantity, having both magnitude and direction.
Q: How does 'q' relate to current?A: Electric current (I) is the rate of flow of electric charge. It's defined as the amount of charge (q) passing a point per unit time (t): I = q/t. So, current is essentially a measure of how quickly electric charge is moving.